Introduction
The gyrations of the U.S. equity market,
particularly as reflected in Standard and Poor’s 500 Stock Index,
have received unremitting attention from academicians and
practitioners alike over the past twenty years. An early, and very
controversial, contribution to this literature was the Modigliani and
Cohn (1979) article in the Financial
Analysts Journal. This article was one of several appearing at the
end of the 1970s to fashion an explanation that linked the two
scourges of that period: high inflation and depressed equity markets.
In a pioneering work in the nascent field of behavioral finance,
Modigliani and Cohn demonstrated how a simple behavioral quirk, “money
illusion” could generate a direct link between high inflation and
undervalued equity.
The form that the money
illusion took was straightforward: an upward movement in inflation
would generate a one-time permanent reduction in nominal accounting
net income without changing the real value of the firm, and this
illusory drop in earnings would trigger a decline in equity values.
The Modigliani-Cohn work ignited a firestorm of research that looked
for purely “rational” explanations for the behavior of the US
equity market. However, for either rational or irrational reasons, the
decline in equity markets ended with the taming of inflation in the
early 1980s and the great rise in valuations since then has coincided
with a continuing long-term decline in inflation.
Equity returns were not the
only asset returns that were affected by inflation. The return on debt
instruments, such as government bonds, was affected in a more direct
and rational manner. As inflation increased beyond the expected
levels, the present value of both the bond coupons and principal
declined, causing the bond to depreciate, frequently more than
offsetting any accrued interest. As inflation declined back to its “normal”
level, the value of the bonds rebounded, generating returns
substantially in excess of the interest payments. Because the decline
in bonds was nearly simultaneous with the decline in stocks and the
subsequent rise in the bonds mirrored a similar rise in stocks, the
correlation of returns between these two assets classes has been quite
high by historical standards since the 1970s. In contrast, during the
1950s it was not uncommon for the returns on stock and bonds to be
somewhat negatively correlated.
The ability to forecast the
future correlation between stock and bond returns is critical to the
practice of asset allocation—the division of assets among different
asset classes based on their anticipated returns and their
correlation. Quantitative approaches to asset allocation have their
roots in the pioneering (and Nobel-prize winning) work of Harry
Markowitz on portfolio optimization. While Markowitz’s model can be
applied directly to the problem of allocating assets between stocks
and bonds, making it a staple
of investments textbooks (see Bodie, Kane, and Marcus, 1996),
practitioners dating back to Grauer and Hakansson (1982) have refined
the basic model in a variety of ways.
[1]
Regardless of the approach that one takes to asset
allocation, it is generally the case the better one is able to
forecast future correlations between the returns in the asset classes,
the greater will be the performance of the portfolio of assets that
one constructs.
This paper will show that the
inflation rate can be an important determinant of the correlation
between stock and bond returns. We refer back to Modigliani and Cohn’s
original model on money illusion as inspiration for a simple
explanation for the linkage between the inflation rate and the
correlation between these returns. It is an important consequence of
their model, not mentioned in the original paper, that any real or
behavioral influence that tends to depress the market’s perception
of equity values will also tend to increase its perception of
financial leverage, which in turn will increase the sensitivity of
equity values to changes in real interest rates. The aggregate equity
market should then be more tightly linked to debt markets during
inflationary times than in noninflationary times.
This paper begins by reviewing
the accounting basis for money illusion and the behavioral link to the
improper valuation of equity. Then, we look at the empirical evidence
that inflation exerts an influence on the correlation between equity
and debt. Finally, we examine both the limitations and potential for
future refinement and application of the analysis.
The Money Illusion
To illustrate the illusion
let us imagine a firm, the demand for whose product is real,
impervious to inflation and in zero growth steady state. While the
reader may have such a firm in mind, we have selected Sewer Security
Ltd. as our example. It is based just outside the City of New York,
has been in business for some 30 years and, by regulation, can service
only the island of Manhattan. That regulation also stipulates that
Sewer Security is the only firm allowed to so service Manhattan. Its
product is designed to prevent rodents and other vermin from gaining
access to buildings through plumbing connections. The device is
guaranteed for five years, and disintegrates in five years and 60
days. Virtually all of their installations are now replacements.
Installation of the replacement takes but minutes, payment is COD, and
prices are set to maintain the firm's operating profit at 50% of
sales. Also, the real value of the physical plant equals the real
value of sales, and the plant depreciates at a constant and continuous
rate of 10% per annum.
The owner is fiscally
conservative. He limits the amount of debt to the book value of Sewer
Security's physical plant. Also, he has observed that upward sloping
yield curves are the norm and, to reduce interest costs, finances his
operations only with floating rate paper.
[2]
The rate on the paper is tied to the rate on
government treasury bills: it changes daily. In a presentation to the
students at a prestigious east coast business school, he noted that
his firm was a real business in that any changes in costs, positive or negative,
are immediately passed on to his customers.
Further, his debt management policy–constant real debt at a
floating rate–together with the firm’s natural advantages, should
leave the real wealth of his debt and equity holders, unaffected by
changes in inflation.
The corporate tax rate is 50%
and the real rate of interest is 4%. Both remain so throughout the
period we examine.
For
ease of exposition, the income statement below starts with sales of
100.
Sewer Security
Income Statement
(Steady
State, No Inflation)
Sales
100
Expenses
50
Operating
Profit
50 [by definition above]
Interest
4
Plant
Replacement
10 [10% of plant (100)]
Net
Before Taxes
36
Let us now assume, at the beginning of the next year,
unanticipated inflation at a continuous annual rate of 20% that
ceases, again unexpectedly, after a year. When we
examine this operation after a year of inflation we find the
following:
Sewer Security
Income Statement
(After
1 Year of Steady State, Unanticipated Inflation at an Annual Rate of
20%)
Sales
110
Expenses
55
Operating Profit
55
Interest
15.2
Plant Replacement
11
Net Before Taxes
28.8
To explain: we grew the sales and expenses in a
lagged response to the unanticipated inflation. Even though sales and
expenses are running at a rate 20% above last year’s by year-end,
the average for the year is only half that. Clearly the ratio of
operating profit to sales is unaffected by inflation.
However, interest expenses
jumped dramatically. Remember, the rate changes daily as a function of
the Treasury bill rate. We assume that rate encapsulates realized
inflation, with a one-day lag, in such a way as to protect the debt
holder from the ravages of inflation. Thus by the end of the year,
lenders will be asking for the 4% real rate plus the 20% inflation to
date. The average for the year can be calculated as the compounding of
the 4% real rate plus the 20% continuously compounded inflation.
Furthermore, any changes in the risk premium will now have a greater
relative impact on earnings. Hence, not only will the value of the
firm be depressed if investors base valuation on earnings, which was
Modigliani and Cohn’s original point, but the apparent increase in
the leverage of the firm, as reflect in its debt/equity ratio, will
make it more interest-rate sensitive. As a result its returns will
correlate more closely with those of debt instruments, which are also
interest-rate sensitive.
Finally, returning to the
income statement, depreciation is 10% of the physical plant, which is
now on the books for 110. We had to continuously replace 10% of the
plant over the year, at an average cost 10% higher than the plant's
book value. The reader will note that earnings (and stock prices, to
the extent that stock prices reflect earnings) decline along with bond
prices as nominal interest rates rise.
We excerpted comments from a
security analyst's report on Sewer Security:
“Sewer Security’s earnings
plummeted 20% in a most disappointing year. Over the years Sewer has
become the prototypical yield stock on which those with income needs
could depend. The past stability of Sewer’s operations has allowed
management to pay out virtually 100% of earnings as dividends year in
and year out. We are at a loss to understand how management can
continue to maintain the dividend at its current rate.
The
main culprit in this tragedy appears to be management’s naive and
shortsighted debt management policy. Interest payments almost
quadrupled with devastating impact on earnings. Unless management gets
a better handle on the principles of corporate finance, this company
is in for some very rocky times.”
Some years later, after inflation had subsided, management presented
the following annual report:
Sewer Security
Income Statement
(Post
the 20% Inflationary Shock, Steady State, No Inflation)
Sales
120
Expenses
60
Operating Profit
60
Interest
4.8
Plant Replacement
12
Net Before Taxes
43.2
The reader can confirm that the Net Before Taxes
of 43.2 is 20% more than the original Net of 36. As expected, on a
point-to-point basis, our firm appears impervious to the ravages of
inflation: however, there is a one to one relationship between the
inflation rate and Sewer Security’s earnings.
We managed to find a security
analyst's comment on this report, which is reprinted below; we were
unable to determine whether it was from the same analyst quoted above.
“Sewer Security's management
pulls off a dramatic turnaround! Earning skyrocketed 51% over the low
of a couple of years ago. Showing confidence in the strength and
quality of their renewed earnings, management raised the firm's
dividend, which is now a full 20% above historic levels.
The focus of this turnaround was
the firm’s debt management policy. Interest payments fell by some
two-thirds from their high with a most favorable impact on earnings.
Management took a strong bet on the level of rates, and it paid off
handsomely!”
To recap, we designed a firm to be impervious to inflation: we
protected it in terms of demand for its product, its costs and its
financial structure. However, this protection failed, and failed
dramatically, during periods with changing levels of inflation.
Accounting Theory
Before we look at the empirical evidence, we
should take a moment to explain what happens to the “earnings”,
and to note a theme in the literature that argues that accounting,
appropriately practiced, should not fall prey to money
illusion.
In correspondence with the
second author (reprinted here in the Appendix), André
Perold at the Graduate School of Business at Harvard University proves
that the observed loss of earnings appears in the properly calculated
value of the plant, exactly as Modigliani and Cohn suggested. But we
note that most accountants do not practice calculus, and it is
unlikely even if they did, that FASB would accept such adjustments.
Fischer Black (1980) and Jack
Treynor (1993) among others, argue that accountants should adjust
earnings to reflect the firm’s underlying value. To quote from
Fischer Black (1980, p. 20), “Security analysts are clearest in
their thinking about earnings, . . . They would like the accounting
process to give an earnings figure they can simply multiply by 10 to
get an estimate of value.” Black then notes that the ratio of price
to earnings is more stable than the ratio of price to book. He argues
that this proves that accountants do attempt to make earnings a
statement of value as opposed to a statement of change in value.
We accept his argument and
evidence. However, price earnings ratios are not constant either
across firms or through time. Accountants may attempt to make earnings
a statement of value but, according to investors, they fail.
The Empirical Evidence: Stock/Bond Correlations and Inflation
Although the procedure for estimating the
variance of a financial time series has received enormous attention,
especially once listed options appeared in the 1970s, the estimation
of covariance or correlation, which is needed to compute the overall
variance and risk profile of a portfolio of assets, is only beginning
to receive serious attention.
[3]
It is common practice to use from 36 to 60 monthly
observations (possibly weighted by a time-decaying factor) to compute
the correlation between two assets classes–in our case the U.S.
stock and long-term government bond returns series that are reported the Stocks,
Bonds, Bills, and Inflation database prepared by Ibbotson
Associates
[4]
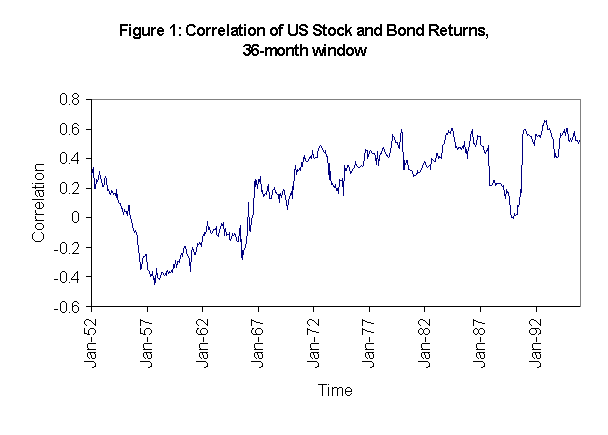
. Figure 1 gives a graph of the 36-month historical
correlation between U.S. stocks and bonds during the post-war period
beginning in 1952. Following the lead of Modigliani, Cohn, and
countless other researchers, we will restrict our analysis to data
taken from this period; to the extent that the analysis has been done
going back to 1926 the additional data tends to “noise up” the
results but not change the basic conclusions. The volatility of this
series indicates, as we shall demonstrate statistically, that past
correlation by itself is of very limited use for forecasting future
correlation.
A natural way to proceed would be to divide the period from 1952 to
1995 into non-overlapping 36-month periods and then determine the
extent to which the correlation during a period depends on the
information available at the beginning of the period; in particular,
the observed correlation for the past period and the rate of inflation
[5]
. An obvious problem with this method is there are only 14
distinct 36-month periods available during the postwar era, too few
from which to draw meaningful statistical conclusions. To get around
this problem we will use two approaches. First, we will use a shorter
12-month window, which will expand the number of observations to a
more comfortable, but still low, 42. Second, we will greatly expand
the number of observations to 400 or more by using monthly overlapping
windows. While this method makes the fullest use of the information
available, it also violates the independence assumptions that underlie
regression analysis, which limits the applicability of the results.
Nonetheless, these two approaches taken together provide some insight
into the correlation between stocks and bonds.
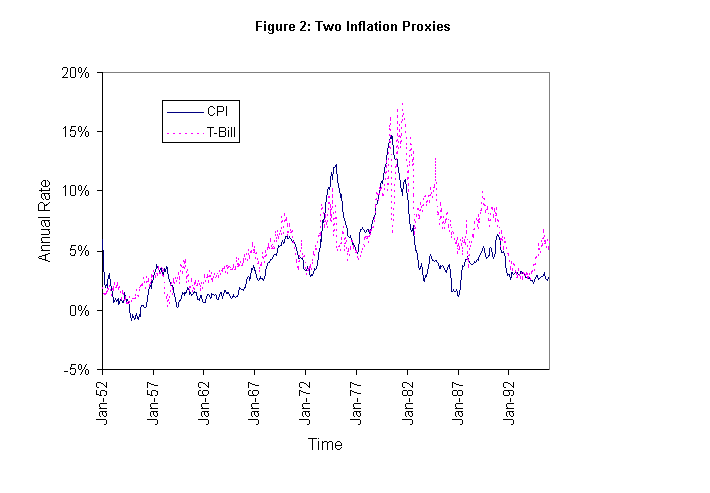
Although the introduction of inflation-indexed
Treasury Bonds in 1996 may ultimately lead to meaningful time series
that give the market expectation of future inflation, for this
analysis we are forced to make do with much less. For the sake of
completeness, we use two separate proxies for inflation. The first
proxy is the one-month Treasury Bill rate reported by Ibbotson. We
convert it from a monthly rate to an annual rate for comparability and
ease of interpretation. As a measure of inflation, the T-Bill rate has
the advantage that it is forward-looking, if only for a month.
However, it has the disadvantage that if the real rate of interest is
nonconstant, which is especially likely during times of active
monetary intervention, it provides a noisy and potentially biased
measure of inflation. The second proxy is the consumer inflation rate
for the previous year (the change in CPI) also as reported by Ibbotson.
(Unlike the T-Bill rate, a single month’s number cannot be used
because of its lack of precision with which it is reported by the
government.) While this proxy is a backward-looking and subject to
substantial measurement error, it does not directly conflate other
macroeconomic variables as does the T-Bill rate. Figure 2 gives a
graph of these two proxies, which closely track one another much of
the time as evidenced by a correlation of 0.7472.
In the absence of any fundamental insight as to how
inflation and historical correlation affect the future correlation
between stocks and bonds, we use a simple linear specification. We
recognize that because correlation is limited to the range of –1.0
to 1.0 that this simplification may lead to misspecification of the
relationship for extreme values of inflation. We accept this
limitation in light of the value of viewing the linear specification
as a convenient first-order approximation to the real relationship.
The regression results for the 12-month windows are
given in Table 1. Each of the 42 windows is constructed to span a
single, complete calendar year. The first regression fits the 12-month
stock-bond correlation to the annual T-Bill rate (for the previous
December) and a constant term. This proxy of inflation by itself
accounts for nearly 36% of the variance in the 12-month stock/bond
correlation. From the equation we see that a 1% increase in the
annualized T-Bill rate leads to rough a 0.07% (or a 7 basis point)
increase in the correlation between stocks and bonds. Looking at the
second and third regressions, the historical correlation (from the
previous 12 months) taken alone explains only 19% of the variance in
correlation and adds only a slight amount to the explanatory value of
the T-Bill rate. The use of the CPI-based inflation measure in place
of the T-Bill in the final two regressions generates results that are
substantially the same with a bit less precision. In all cases, the
t-statistics for the coefficients of the two inflation proxies, which
appear in parentheses under the coefficients, are significant at well
beyond the 99% level. A regression with both inflation proxies
included is presented neither here nor later in this paper because the
high degree of collinearity between the two proxies, as noted above,
makes the output of this regression of little additional value.
T-Bill
Change in Prior Year’s
Constant
rate
CPI
Correlation
d
R2
-0.1790
7.0924
1.7970
0.3596
(-1.8381)
(4.7391)
0.1244
0.4395
2.3307
0.1921
(2.0022)
(3.0843)
-0.1582
6.0193 0.1765
2.2459
0.3823
(-1.6077)
(3.4654)
(1.1987)
-0.0563
6.6334
1.5732
0.3306
(-0.7077)
(4.4443)
-0.0590
5.4656
0.2288
2.2217
0.3724
(-0.7567)
(3.3470)
(1.6126)
Table 1: Regressions for predicting the monthly stock/bond correlation
for non-overlapping 12-month annual windows from 1953 to 1995.
(T-statistics are in parentheses, d
is the Durbin-Watson statistic, and N=42.)
Because the three time series under consideration—stock/bond
correlation, T-Bill rates, and consumer inflation—are all time
series that tend to trend upward over the time period under
consideration, one must be alert to the possibility of spurious
regression, the tendency for regressions between macroeconomic time
series to show significant relationships caused by the violation of
the assumptions of the regression model rather than any true
relationship between the variables. Fortunately, there is no evidence
of spurious regression any of the regressions in Table 1: the
Durbin-Watson statistics show no undue correlation of the residuals
(for spurious regressions the Durbin-Watson statistic is often less
than the R2) and the dependent variable, stock/bond
correlation, as the second regression equation indicates, does not
have a unit root.
[6]
The second approach to estimating stock/bond
correlations, which uses overlapping windows, exhibits low
Durbin-Watson statistics, one of the symptoms of spurious regression.
This is simply an artifact of the overlap in the data. The inputs used
to compute the correlation for two successive months will be the same
except for the latter will drop the oldest stock and bond return
observation and replace it with the stock and bond returns for the
current period. This will automatically generate high autocorrelation
in the stock/bond correlation time series and the degree of
autocorrelation will increase with the size of the window.
Table 2 repeats the five regressions done for the
non-overlapping windows in Table 1 for 12-month, 36-month, and
60-month correlations. The top set of five regressions, which cover
the 12-month correlations over 504 monthly observations show little
change in results except that the t-statistics are all much larger and
the Durbin-Watson, which is not included in the table, is near 0.2 for
the 12-month regressions and near 0.1 for the others. Comparing the
results in Tables 1 and 2 we find that for a 12-month window the
additional information contained in monthly observations may generate
somewhat more accurate estimates of the parameter coefficients;
however, it is difficult to gauge that accuracy because the
autocorrelation in the errors leads to an overstatement of the
t-statistics.
[7]
Indeed, had we not run the nonoverlapping regression first,
these overlapping regressions would at first glance appear to be
spurious.
T-Bill
Change in
Prior Year’s
Months Constant
rate
CPI
Correlation N
R2
12 -0.1646
6.8761
504
0.3180
(-5.8068)
(15.2998)
12
0.1175
0.4614
504
0.2118
(6.8276)
(11.6140)
12 -0.1365
5.4371
0.2487
504
0.3656
(-4.9191)
(11.0226) (6.1326)
12
-0.0421
6.0002
504
0.2524
(-1.7231)
(13.0197)
12 -0.0389
4.4723
0.3019
504
0.3267
(-1.6765)
(9.24715)
(7.4341)
36
-0.0897
5.8388
456
0.4271
(-4.2989)
(18.3966)
36
0.1248
0.6526
456
0.4767
(11.1179)
(20.3367)
36
-0.0401
3.5134
0.4489
456
0.5849
(-2.2068)
(10.8665)
(13.1239)
36
0.0224
5.0369
456
0.3460
(1.2456)
(15.4988)
36
0.0243
2.8750
0.5016
456
0.5639
(1.6551)
(9.5187)
(15.0454)
60
0.0274
4.2565
408
0.4428
(1.6891)
(17.9624)
60
0.1832
0.5669
408
0.5645
(23.1364)
(22.9407)
60
0.0914
1.9579
0.4166
408
0.6185
(6.4321)
(7.5717)
(13.6578)
60
0.1144
3.6097
408
0.3478
(8.0791)
(14.7132)
60
0.1328
1.4504
0.4644
408
0.6022
(11.9308)
(6.1956)
(16.0951)
Table
2: Regressions for predicting the monthly stock/bond correlation for
overlapping windows in the postwar period (t-statistics in
parentheses).
The results in Table 2 for the 36-month and 60-month
correlations are qualitatively similar to the 12-month correlation,
only the overall fit and the precision of the coefficient estimates is
better. This is to be expected given that the longer windows make the
measurement of correlation less noisy. Also, the correlation for the
prior window now predicts future correlation better than does either
of the inflation proxies. As before, there is little difference in
explanation power between the two measures of inflation, the T-Bill
performs minimally better than the CPI. The important thing is that
inflation, either alone or in combination with the past correlation,
significantly aids in the prediction of future correlation between
stocks and bonds over the sample period (and there is no basis in
received theory for this to happen).
Interpreting and Extending the Results
Methodologically, this paper should be considered
as a point of departure for further investigation into the nature of
stock/bond (and other asset) correlations. We hope to have opened
Pandora’s Box just a bit and to have avoided the temptations of “data
mining” in that we did not try to find the “best” estimate of
stock/bond correlation. Clearly, inflation is not the only factor to
effect the real or perceived aggregate leverage of S&P 500 firms.
Growth in the interest-sensitive financial services sector, from its
inclusion in the S&P 500 in 1976 to the present, and the fact that
major S&P 500 companies such as General Electric, General Motors,
and Ford have significant financial subsidiaries, may underlie an
apparent secular uptrend in stock/bond correlations that this analysis
does not directly take into account.
[8]
However, starting with the
insight that money illusion would affect not only the value of equity
but also the correlation of its returns with debt returns we found
empirical evidence to support the expected linkage between inflation
and stock/bond correlations. While we have not derived a precise
measurement of stock/bond correlation and inflation, the linkage is
robust to alternative methods for measuring both. The straightforward
analysis performed in this paper is not put forth as definitive proof
that money illusion drives equity valuation; instead, we demonstrate
that a simple behavioral model can provide a fuller understanding of a
neglected area—the correlation between stock and bond returns.
The main empirical message of
this paper is that asset allocators, whose performance ultimately
depends on their ability to forecast asset correlations accurately,
need to look beyond historical returns time series to macroeconomic
and other variables in making their projections. The effect of
inflation on equity values, through money illusion or a related
mechanism, is enough to justify its incorporation into any estimate of
stock/bond correlation. It almost goes without saying that similar
effects are likely to affect the correlations between other pairs of
asset classes.
APPENDIX
[9]
Definitions
and Assumptions:
Pt = plant at time “t”
St
= sales running rate = Pt by assumption
Bt
= bonds outstanding = Pt by assumption
Ct
= cumulative cash flow from 0 to “t”, C0= 0
i =
inflation rate (constant)
g = profit
margin (gross, before interest and depreciation
[depreciation
= plant ‘maintenance’])
y = real
rate of interest
r = nominal
rate of interest = i+y
m =
maintenance rate
Model:
Plant grows
with inflation: dP/dt = i
=> Pt = P0eit = St
= Bt
(1)
Cash Flow:
dC/dt = gSt - mPt - rBt + iPt
+rCt
(2)
Where: gSt
= gross profit
mPt = maintenance expenditures
rBt = interest on debt
iPt = gain in nominal value of plant
= increased borrowings which are ‘dividended’ out
rCt = reinvestment of cash flow at rate r (in a
money market fund)
therefore
dC/dt = (g - m + i - r) * Pt + rCt
(3)
substitute r = i + y and,
dC/dt
= (g - m - y) * P0eit
+ (i + y) * Ct
(4)
Note the inflation gain in the plant is canceled by
the inflation component of the nominal rate.
The
solution to the differential equation (4) is
Ct = (g - m - y) * P0eit * ((eyt
- 1)/y)
(5)
To
calculate the present
value of this cash flow, note that $1 growing at rate r grows to ert
by time “t”
Therefore the Value of the Firm =
e-rt
* Ct = e-(i+y)t * Ct = (g - m - y) *
P0 *((1 - e-yt )/y)
(6)
Notes:
1.)
Inflation i affects only the plant = P0eit
and hence the cash flow Ct
in (5)
However, i disappears from value in (6)
2.)
Reinvestment
of cash flow at rate r is needed only to calculate the present value
of the cash flow. If
the cash is dividended out, the accounting numbers are as follows (for
the period 0 to t):
Sales = òoT
S(t)/dt = òoT
P0eit dt = P0 * ((eit -
1)/i) = P0*a where
a = ((eit - 1)/i) (7)
Gross
Profit = g * P0*a
Maintenance = m * P0*a
Interest Expense = (i + y) * P0*a
Inflation Gain in Plant = i * P0*a
Accounting
Net Income = (g - m - i - y) * P0*a
Economic Net Income = (g - m - i - y + i) * P0a
= (g - m - y) * P0*a